ಠ_ಠ偷偷說
#噗幣轉蛋
各位大學生們來展現自己的微積分能力吧
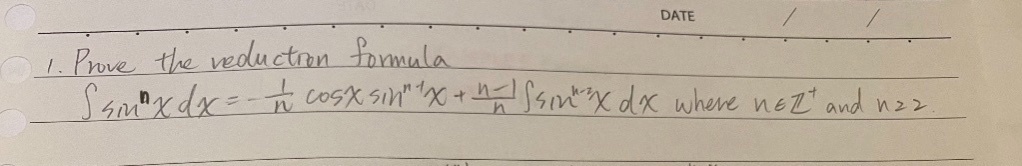
第一題是證明題，收第一個解出來的旅人們
解出來後可投1
，掉落物不明，不過會是我有在接委託的可愛模板
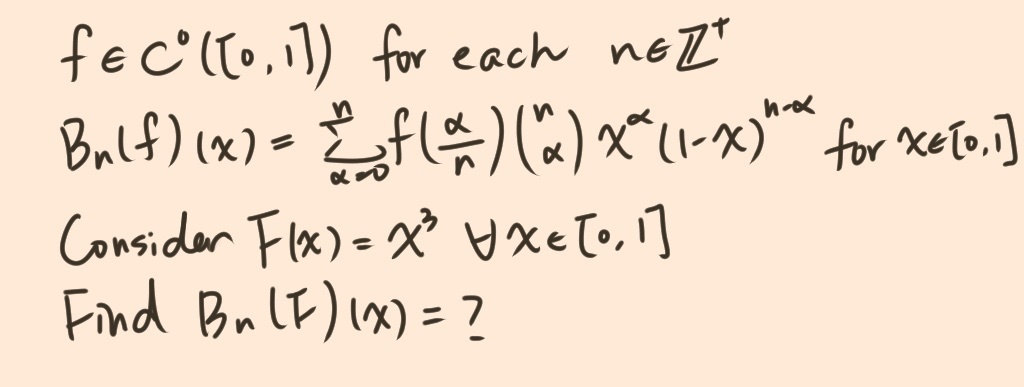
第二題是bonus，不用投幣，也會掉一樣的東西
掉蛋時間兩週內，歡迎旅人們來挑戰
各位大學生們來展現自己的微積分能力吧
第一題是證明題，收第一個解出來的旅人們
解出來後可投1
，掉落物不明，不過會是我有在接委託的可愛模板第二題是bonus，不用投幣，也會掉一樣的東西
掉蛋時間兩週內，歡迎旅人們來挑戰
62 responses
？！
等我一下
謝謝旅人 
可……可惡，認錯人
如果可以動用其他結論的話，第二題可以把n^(-3)提出，可再轉化題目成算二項分布的三階中心矩
靠查表找偏度，算(或是直接去找)可得E([X-mu]^3)=-np(1-p)(2p-1)，這裡X是隨機變數，p是機率(就是題目的x)
我們已知二項分布的各種中心矩，剩下的就是純計算出E(X^3)=-np(1-p)(2p-1)+3n^2·p^2(1-p)+n^3·p^3
得B_n(F)(x)=(-nx·(1-x)(2x-1)+3n^2·x^2(1-x)+n^3·x^3)/(n^3)
靠查表找偏度，算(或是直接去找)可得E([X-mu]^3)=-np(1-p)(2p-1)，這裡X是隨機變數，p是機率(就是題目的x)
我們已知二項分布的各種中心矩，剩下的就是純計算出E(X^3)=-np(1-p)(2p-1)+3n^2·p^2(1-p)+n^3·p^3
得B_n(F)(x)=(-nx·(1-x)(2x-1)+3n^2·x^2(1-x)+n^3·x^3)/(n^3)
加了·在中間
您好強 
