是嗎?

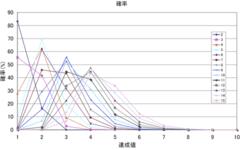
從此表上可以看到，左側系統的消耗資源轉骰成功率提升以常用區間而言，大約落在35~40%左右。基本上可以說有決定性的差異。

相對比右側的DF，基本上幾乎是要等於DF+2才有的效果了。

雖左側看起來基礎成功率低，但反過來說更是算強迫人要多使用「消耗資源轉骰」的行為。

以數據驗證上，明顯是左邊轉骰的效益比較高。其他機制面上的東西我是不清楚，不過機率數據可以供大家參考看看。

(這大概是繼上次算DX3rd的骰子跟傷害期望值以來讓我最燒腦的一次)

ㄟ，因為他在骰面和為3的狀況，是達成值會是讀作0，所以你這算的只是骰面讀數，而不是達成值。像是你左側圖表第七欄的次數欄，在達成值為3的那一項，要被移動到達成值為0。

然後在第三欄的部分，你忽略了陰德值除了用來可以±1骰面，還可以將達成值直接+1。不過其實就是誤差大概20-30個事件，影響不大。

欸，原來可以直接+-1，而不是只能改骰子嗎？

都可以

這樣要出現一項13的耶

嘿啊，還有21的

21的可以忽略拉XD

改這個挺快的，我修正一下

所以可以做的變化有 4種增加骰面、4種減少骰面、跟1種增加達成值，再加上原來的取優。

我昨天也是發了之後被朋友指出來，因為我當初也漏看那個規則XD

每讀一次規則就修一次計算，我們大概重複了五次左右吧w

(我沒書只是聽人說

而且這部分對整體分布影響不大，所以結論的部分，我跟你的一樣，就是裸骰的不利分布，會造成有更大誘因迫使人耗用陰德值來去，讓分布變回其他大部分系統採用的常態分布。

(好，我改好了

欸靠北

傳錯

還有骰面合為3的戲劇性失敗不能調。

jamesragnarok1992: 原來不是每個都可以調整阿，好，這樣要修的真多

這機率怎麼這麼麻煩

這是規則書93頁的文字，我剛發現好像跟111頁有微妙出入
可能在跟作者確定一下比較好(不含誤植的+-1 這邊我看達成植可以到+2

你們不要害我一直改數據啦！

幫你整理一下(如果我沒讀錯的話)：
四骰相同算20，一對算另兩骰合，兩對取高，一對三點算零，其餘算零。
一點數可以使一顆骰骰面加減一，或是達成值加一。

總之我先以轉1個、達成值+1、骰面3的不能轉為基準的圖是這樣。

我想大方向還是差不多啦。

不過可以+2的話那整個要重算很多，+1影響不太大。

(先這樣吧，這系統的機率真的難算的太崩潰

其他地方都是寫加一，我懷疑是p.93寫錯。

我剛連絡上作者了，轉骰的+-是p93正確
但達成值只+1，所以達成值是p93錯



這是p111（勘誤有寫說要+-1，所以轉骰可以+也可以-

說起來，其實之前看歌風雖然本來要做的，
結果有看到別人的統計結論我就沒做了。

順邊丟一下歌風的

ウタカゼ　判定の達成値 - 戯言

他這個網站有很多有趣的機率驗證
包含DX3、神我狩、SW2.0的威力表等等

歌風的對骰和龍骰期望值曲線幾乎是一樣的，當初看到真的很驚訝

然後說說這次的土法處理。
首先是當然是智障的把1296個組合x8種換骰，每組取最高的那個統計出來。(實際上不一定有8種，1跟6都是只有+1或-1的)

但由於這樣實在太蠢了，所以第二次的土法稍微改進。
因為排列順序不影響結果(比如說1356跟1653)的組合都是會得到一樣結果的，並起來變成同一個組別(之後在x排列可能數即可)。
可以從1111~6666變為只剩下126個組別。

到這個時候已經被簡單化為可以人力計算的東西了，所以也就很自然的能一目瞭然

不過如果可以轉兩顆的話可能這問題就會變得複雜多一些。
(但依然只是選擇問題，每個組別的幾種可能都列出來取高即可)
不過簡化成126個組別後，基本上使用人力看也不是很費力。

不過若讓1或6加減1是可以變成6或1的話，
這次的問題又會更好玩一點點，大概是這樣，大家也可以回家玩看看(不

另，如果想用excel處理這個方法的話其實是只需要把每個組別分類成
AAAA、AAAB、AABB、AABC跟ABCD五種類別構造而已。

實際上骰面減一只有要湊出一色時才會用到(2223改成2222等)，其餘的接用骰面加一即可。另外在一對時改骰面且不會成為新的特殊組合時，骰面加一和達成值加一的效果是一樣的，只有在達成值本來就在18、20兩個上限時才有差別。

當發現可以直接分類成五個大類別後，就會發現這個問題的處理難度開始大幅下降，剩下的就是單純地對每個類別做處理即可了。

這個算是滿不錯的溫習數學問題，排列組合的好玩之處

不好玩。

比如說AAAB的改骰只要考慮是否A跟B差1而已。
如果是，那把B變成A即可。
若不是，那就取剩下的A+B再+1後就完成這次的改骰處理。
(此時若超過12就取12，如果是可以增加達成值情況就無需設定此限制)

AABB則是直接比較AB大小，然後把大者+1後同上處理即可完成

剩下較為複雜的就是AABC跟ABCD的情況，這個由於我還沒想到比較好的過濾手法，所以就直接把全部操作並列出來取高了。

但有閒的時候應該會再改進選擇的手段。

另，會出現取完後結果為合計3的情況必然是
剩下的2個是1跟2。(的AAAB或AABC)
所以只要把有含1與2的組合先經過一次這個過濾就可以篩出這些個組合了。

jamesragnarok1992: 哪有，超好玩的。

解開來的時候就覺得超爽的

發覺自己跟高中時代相比沒有長進哪，超不好玩。

話說回來要不是這系統我還不會算十八啦的機率。

下次可以挑戰看看dx3的期望值計算，那個真的超歡樂

有人算過的東西查出來就好了。(怠惰

之前是處理跟兩手武器有關的東西吧，我記得

一時之間找不到XD

(開始一篇一篇看

找到了，12年前的文章w，算命中率的
討論在雙手持武器命中受-2懲罰的情況時
命中與對方迴避基準值在不同差異下雙手和單手持武的傷害期望
ソード・ワールド2.0　両手利きについて - 戯言